Técnicas Sudoku avanzadas
En esta sección se presentan las estrategias avanzadas que se utilizan para resolver sudokus. Estos métodos son necesarios para resolver los sudokus más difíciles. Se centran en el uso de los números candidatos y cómo poder eliminarlos usando sólo la lógica. También puedes leer las Técnicas Sudoku para ubicar un número de forma directa.
- 1. Terminología
- 2. Uso de números candidatos
- 3. Individuales
- 4. Intersección Línea-Región
- 5. Subconjuntos desnudos
- 6. Subconjuntos ocultos
- 7. Intersección Fila-Columna
- 8. Cadenas coloreadas
- 9. Par remoto
- 10. XY-Wing
- 11. XYZ-Wing
- 12. Cadena XY
- 13. Rectángulo de unicidad
Terminología
Tablero de juego: cuadrícula de 9x9 casillas, es decir 81 casillas.
Casilla: elemento individual del tablero de juego que contiene los números del 1 al 9, cada casilla está inserta en una fila, en una columna y en una región simultáneamente.
Valor: número contenido en una casilla.
Ubicar: colocar con seguridad un valor en una casilla.
Fila: línea de 9 casillas de forma horizontal.
Columna: línea de 9 casillas de forma vertical.
Región: recuadro de 3x3 casillas (9 casillas).
Línea: fila o columna, hay 18 líneas en un sudoku.
Grupo: fila, columna o región, en un sudoku hay 27 grupos.

Coordenadas
Fila: se representa con los números del 1 al 9.
Columna: se representa con las letras de la A a la I.
Región o recuadro: se representa de R1 a R9.
Casilla: se representa con la intersección columna-fila. Ej: D6.
Uso de números candidatos
La utilización de candidatos es fundamental para solucionar los sudokus más complejos.
Definiciones
Marcas de candidatos: anotaciones que se hacen en la parte superior de las casillas, consistentes en colocar los números posibles de las mismas, es decir los candidatos.
Candidato: cada uno de los números posibles de una casilla.

En la imagen de arriba se ve el tablero sin marcas de candidatos. En la imagen de abajo se ve el tablero con las marcas de candidatos.
Relaciones
En los métodos que veremos a continuación hay una interacción entre tres elementos:
- Grupos
- Casillas
- Candidatos
Relaciones entre los elementos:
- Grupos entre sí
- Casillas entre sí
- Casillas con grupos
- Candidatos entre sí
- Candidatos con casillas
- Candidatos con grupos
Individuales
Estos métodos sirven para ubicar con certeza un número para una casilla.
Único desnudo
Es cuando en una casilla solo hay un candidato. Al ser el único número posible, ese candidato es el valor para esa casilla.
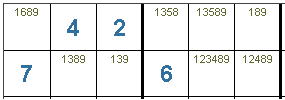
Único desnudo. En el ejemplo la casilla D1 tiene un solo candidato, al ser el único valor posible, en D1 va ubicado el valor 3.
Único oculto
Es cuando existe un solo candidato para un grupo (fila, columna o región), además, éste candidato se encuentra dentro de la casilla junto con otros candidatos, es por esto que se dice que es oculto. Al ser el único número posible dentro del grupo, ese candidato es el valor para esa casilla.
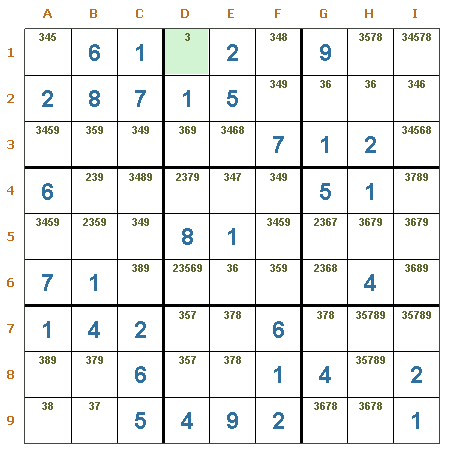
Único oculto por región. La región 1, contiene una casilla (B3) con los candidatos 6 y 7. El 6 es el único candidato para esta región, por lo tanto, la casilla B3 tendrá ubicado el 6 como valor.
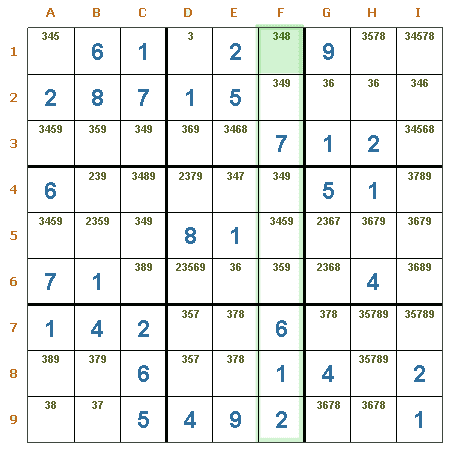
Único oculto por columna. En la casilla F1 de la columna F, se puede apreciar que el 8 es el único candidato para &esta fila. Por lo tanto, la casilla F1 tendrá al 8 como valor.
Intersección Línea-Región
Hasta ahora los métodos usados han servido para ubicar valores de forma segura en las casillas. Cuando no se puede ubicar más números de forma segura hay que empezar a eliminar los candidatos.
Dada una intersección entre un grupo (1) y un grupo (2), es decir cuando hay casillas comunes para los dos grupos, se dice que hay una intersección Línea-Región cuando un candidato que pertenece a la intersección está restringido para el grupo (1), es decir en algunas de las casillas de la intersección debe ser ubicado como valor. Por lo tanto, ese candidato puede ser eliminado con seguridad del resto de las casillas del grupo (2).
Intersección Región/Línea
Cuando un candidato está restringido a una línea (fila o columna) dentro de una región, alguna de casillas de la intersección debe contener como valor a ese candidato, por ello ese candidato puede ser eliminado de las casillas de esa línea fuera de la región.
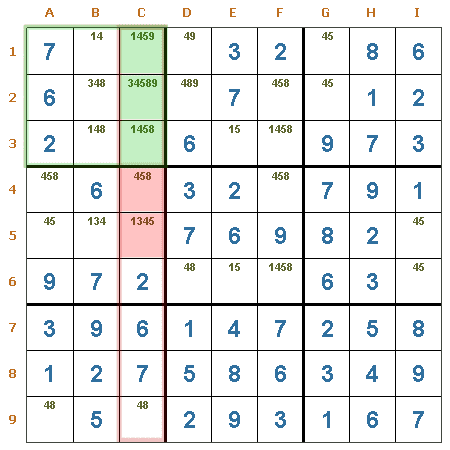
Intersección región/columna. En la región R1, el candidato 5 se encuentra en las casillas C1, C2 y C3, como es obligatorio que sea ubicado como valor en alguna de esas casillas, puede ser eliminado de las restantes casillas de la columna C. Por lo tanto, el candidato 5 se puede eliminar con seguridad de las casillas C4 y C5

Intersección región/fila. En la región R5, el candidato 3 se encuentra en las casillas E4 y F4, como es obligatorio que sea ubicado como valor en alguna de esas dos casillas, puede ser eliminado de las restantes casillas de la fila 4. Por lo tanto, el candidato 3 se puede eliminar con seguridad de la casilla B4
Intersección Línea/Región
Cuando un candidato está restringido a una región, dentro de una línea (fila o columna), alguna de las casillas de la intersección debe contener como valor a ese candidato, por ello ese candidato puede ser eliminado de las casillas de esa región fuera de la línea.
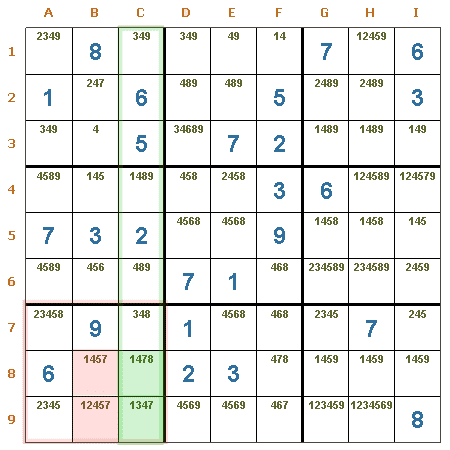
Intersección columna/región. En la columna C, el candidato 7 se encuentra en las casillas C8 y C9, como es obligatorio que sea ubicado como valor en alguna de esas dos casillas, puede ser eliminado de las restantes casillas de la región R7. Por lo tanto, el candidato 7 puede ser eliminado con seguridad de las casillas B8 y B9
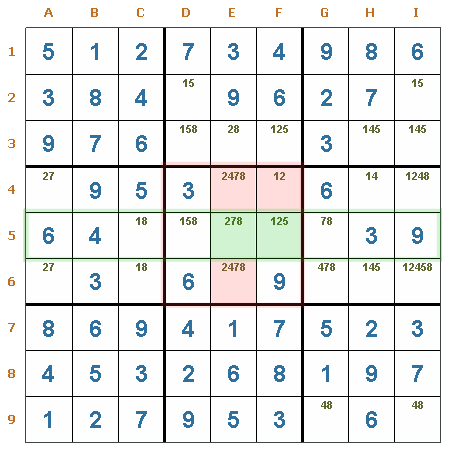
Intersección fila/región. En la fila 5, el candidato 2 se encuentra en las casillas E5 y F5, como es obligatorio que sea ubicado como valor en alguna de esas dos casillas, puede ser eliminado de las restantes casillas de la región R5. Por lo tanto, el candidato 2 puede ser eliminado con seguridad de las casillas E4, E6 y F4.
Subconjuntos desnudos
Hasta ahora solo se ha trabajado con un solo candidato, los métodos siguientes trabajan con grupos de 2 o más candidatos.
Un subconjunto contiene un cierto número de candidatos y el mismo número de casillas que pertenecen a un único grupo.
En un subconjunto desnudo las casillas que pertenecen al grupo solo permiten a los candidatos del subconjunto. Por lo tanto, los candidatos del subconjunto pueden ser eliminados de todas las casillas del grupo fuera del subconjunto.
Par desnudo
Si dos casillas de un grupo contienen a un par idéntico de candidatos y únicamente esos dos candidatos, ninguna otra casilla de ese grupo podría tener esos valores, ya que un candidato tendrá que ir como valor en una casilla y el otro candidato deberá ir en la otra casilla. Por lo tanto, esos dos candidatos pueden ser eliminados de las restantes casillas del grupo.
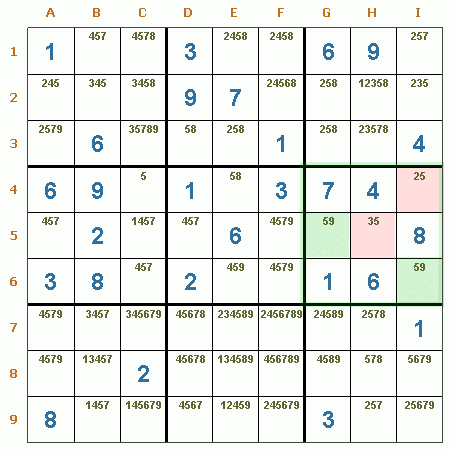
Par desnudo en una región. Aquí se puede apreciar que en la región R6 hay dos casillas, G5 y I6 que tienen un par de candidatos iguales, estos son el 5 y 9. Estos forman un par desnudo, Por lo tanto, se puede eliminar con seguridad el candidato 5 de las casillas H5 y I4.
Par desnudo en una columna. En la columna G se puede ver que existen dos pares de números (5 y 6), en G5 y G8. Por lo tanto, se pueden eliminar los candidatos 5 y 6 de G6, y el 6 de G4.
Trío desnudo
Consiste en tres casillas en un grupo que contienen los mismos tres candidatos. Los candidatos del trío que se encuentran en otras casillas del grupo pueden ser eliminados. Las casillas que componen el trío no necesariamente deben tener a los tres candidatos del trío. Por ejemplo, si un trío está compuesto por los candidatos 1, 2 y 3, las combinaciones válidas para ese trío serían:
|
Casilla A |
Casilla B |
Casilla C |
|---|---|---|
|
123 |
123 |
123 |
|
123 |
123 |
12 |
|
123 |
123 |
13 |
|
123 |
123 |
23 |
|
123 |
12 |
13 |
|
123 |
12 |
23 |
|
123 |
13 |
23 |
|
12 |
13 |
23 |
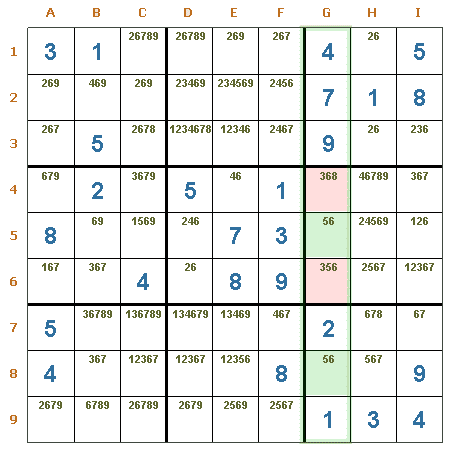
Trío desnudo en una región. En las casillas A9, B9 y C9 de la región R7, puede verse el trío 3, 5 y 9. Por lo tanto, pueden eliminarse con seguridad los candidatos 3 y 5 de A8, 5 y 9 de C7 y 3 y 5 de C8
Trío desnudo en una fila. En las casillas C1, D1 y E1 de la fila 1, puede verse el trío 3, 4 y 9. Por lo tanto, pueden eliminarse con seguridad los candidatos 3, 4 y 9 de A1, 4 de F1 y 4 y 9 de I1.
Cuarteto desnudo
Consiste en cuatro casillas en un grupo que contienen los mismos cuatro candidatos. Los candidatos del cuarteto que se encuentran en otras casillas del grupo pueden ser eliminados. Las casillas que componen el cuarteto no necesariamente deben tener a los cuatro candidatos del cuarteto.
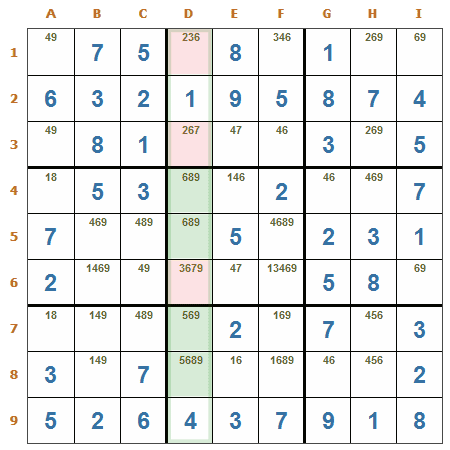
Cuarteto desnudo en una columna. En las casillas D4, D5, D7 y D8 de la columna D, puede verse el cuarteto 5, 6, 8 y 9. Por lo tanto, pueden eliminarse con seguridad los candidatos: 6 de D1, 6 de D3 y 6 y 9 de D6
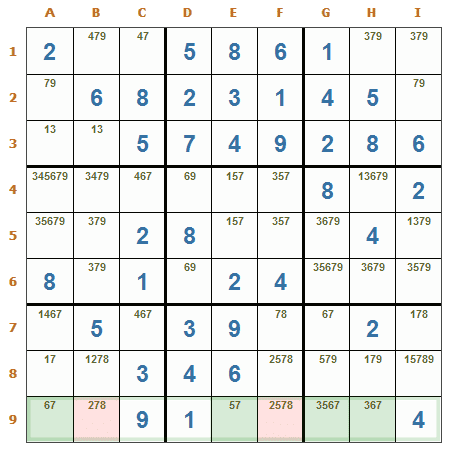
Cuarteto desnudo en una fila. En las casillas A9, E9, G9 y H9 de la fila 9, puede verse el cuarteto 3, 5, 6 y 7. Por lo tanto, pueden eliminarse con seguridad los candidatos: 7 de B9 y 5 y 7 de F9.
Subconjuntos ocultos
Un subconjunto contiene un cierto número de candidatos y el mismo número de casillas que pertenecen a un único grupo.
En un subconjunto oculto las casillas que pertenecen al grupo tienen a los candidatos del subconjunto y a otros candidatos, pero los candidatos del subconjunto no pueden estar en las otras casillas del grupo. Por lo tanto, en casillas del subconjunto pueden eliminarse todos los candidatos que no pertenecen al subconjunto.
Par oculto
Si dos casillas de un grupo contienen un par idéntico de candidatos que no aparecen en ninguna otra casilla de ese grupo, entonces los demás candidatos de esas dos casillas pueden ser eliminados con seguridad.
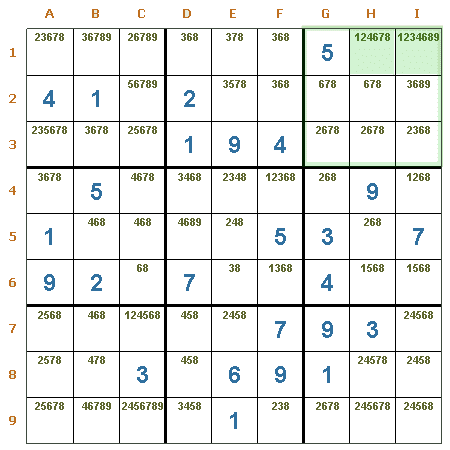
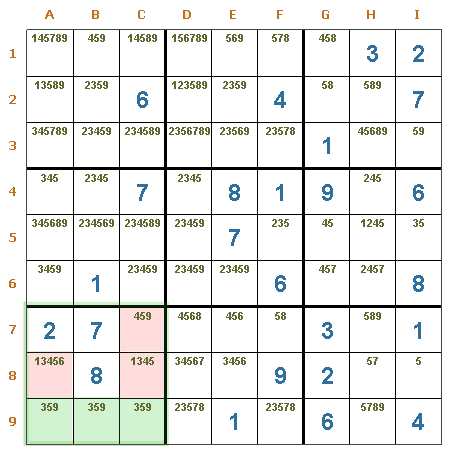
Par oculto en una región. En las casillas H1 y I1 de la región R3 hay un par idéntico de números, estos son el 1 y 4. Por lo tanto, se pueden eliminar con seguridad los candidatos 2, 6, 7 y 8 de H1 y los candidatos 2, 3, 6, 8 y 9 de I1.
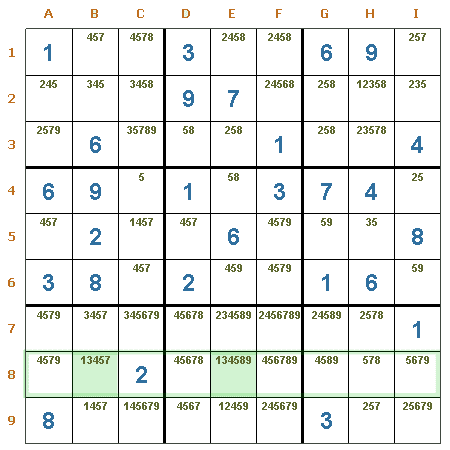
Par oculto en una fila. La fila 8 tiene dos casillas (B8 y E8) con un par idéntico cada una, éste par es el 1 y 3. Se pueden eliminar con seguridad los candidatos 4, 5 y 7 de B8 y los candidatos 4, 5, 8 y 9 de E8.
Trío oculto
Si tres candidatos están restringidos a tres casillas de un determinado grupo, entonces todos los demás candidatos de esas tres casillas pueden ser eliminados. Las casillas que componen el trío no necesariamente deben tener a los tres candidatos del trío. Por ejemplo, si un trío está compuesto por los candidatos 1, 2 y 3, las combinaciones válidas para ese trío serían:
| Casilla A | Casilla B | Casilla C |
| 123 | 123 | 123 |
| 123 | 123 | 12 |
| 123 | 123 | 13 |
| 123 | 123 | 23 |
| 123 | 12 | 13 |
| 123 | 12 | 23 |
| 123 | 13 | 23 |
| 12 | 13 | 23 |
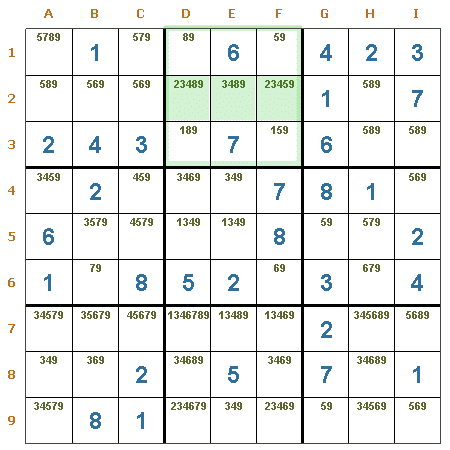
Trío oculto en una región. En la región R2 puede verse que hay un trío oculto en las casillas D2 (candidatos 2, 3 y 4), E2 (candidatos 3 y 4) y F2 (candidatos 2, 3 y 4), Por lo tanto, en esas casillas pueden eliminarse con seguridad los restantes candidatos. En D2 se eliminan el 8 y 9, en E2 se eliminan el 8 y 9, y en F2 se eliminan el 5 y 9.
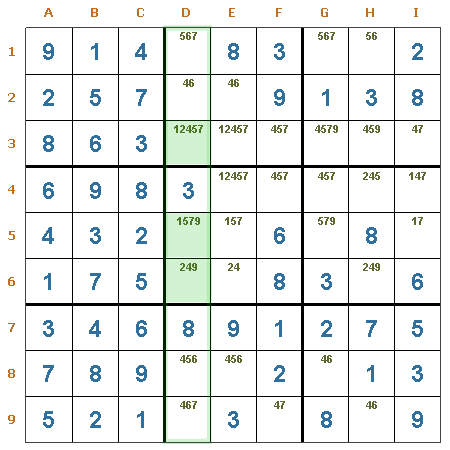
Trío oculto en una columna. En la columna D puede verse que hay un trío oculto en las casillas D3 (candidatos 1 y 2), D5 (candidatos 1 y 9) y D6 (candidatos 2 y 9), Por lo tanto, en esas casillas pueden eliminarse con seguridad los restantes candidatos. En D3 se eliminan el 4, 5 y 7, en D5 se eliminan el 5 y 7, y en D6 se elimina el 4.
Intersección Fila-Columna
En los últimos métodos vistos se trabajaba con grupos de candidatos. Ahora volvemos a trabajar con un solo candidato.
Cuando un candidato está N veces en N columnas (o filas) y también se encuentra en N filas (o columnas), ese candidato puede ser eliminado de todas las casillas vacías de las N filas (o columnas) a excepción de las casillas comunes a las N columnas (o filas).
X-wing
Dado un candidato determinado, en este método se requiere que dos filas (o dos columnas) que contengan cada una dos casillas y sólo dos casillas con ese candidato, y dichas casillas deben compartir las mismas dos columnas (o dos filas) formando un rectángulo. Estas cuatro casillas son las únicas posibles para ese candidato dentro de esas dos filas (o dos columnas). Entonces ese candidato puede ser eliminado de cualquier casilla de las dos columnas (o dos filas) a excepción de las casillas comunes con las dos filas (o dos columnas).

X-wing fila/columna. En el ejemplo puede verse que para la fila 4, casillas C4 y H4, debe ir obligadamente un 4 en una de esas dos casillas, lo mismo ocurre para la fila 8, casillas C8 y H8, por ese motivo en el resto de las casillas de las columnas C y H puede eliminarse el candidato 4, más precisamente de las casillas C7, H7 y H2.
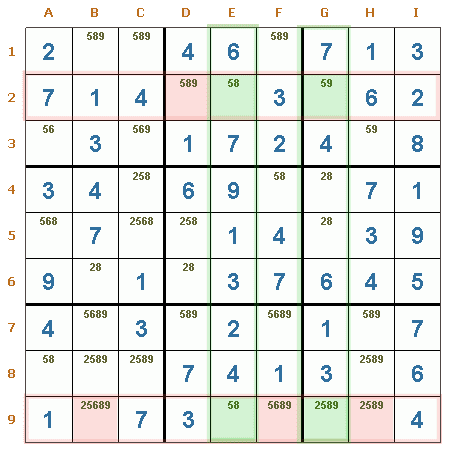
X-wing columna/fila. En el ejemplo puede verse que para la columna E, casillas E2 y E9, debe ir obligadamente un 5 en una de esas dos casillas, lo mismo ocurre para la columna G, casillas G2 y G9, por ese motivo en el resto de las casillas de las filas 2 y 9 puede eliminarse el candidato 5, más precisamente de las casillas D2, B9, F9 y H9.
Pez espada
Es como el X-wing pero con tres líneas (filas o columnas), es decir, tres filas (o columnas) que contienen cada una de ellas no más de tres casillas, con un candidato determinado, y compartiendo todas ellas no más de tres columnas (o filas). Estas forman una cuadrícula de hasta nueve casillas que son las únicas posibles para el candidato en esas tres filas (o columnas). Cualquier candidato que esté dentro de esas tres columnas (o filas), a excepción de las casillas de la cuadrícula, puede ser eliminado.
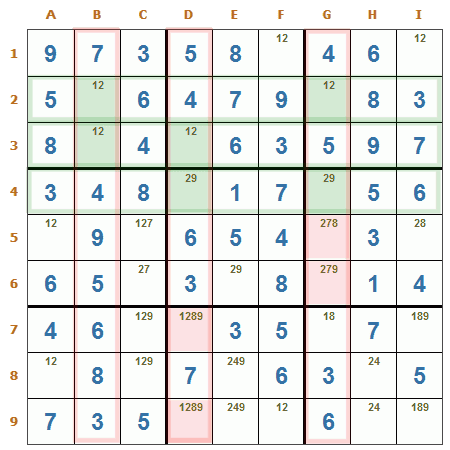
Pez espada fila/columna. En el ejemplo puede verse que para la fila 2, casillas B2 y G2, debe ir obligadamente un 2 en una de esas dos casillas, lo mismo ocurre para la fila 3, casillas B3 y D3, y la fila 4, casillas D4 y G4, por ese motivo en el resto de las casillas de las columnas B, D y G puede eliminarse el candidato 2, más precisamente de las casillas D7, D9, G5 y G6.
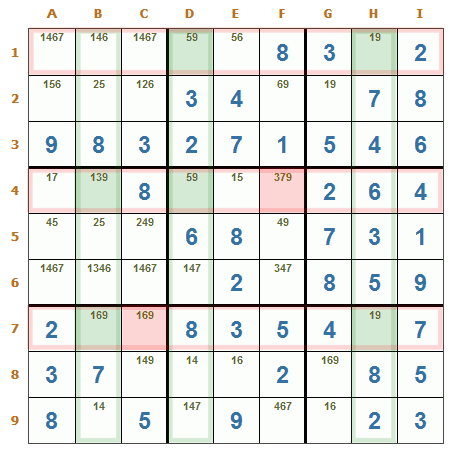
Pez espada columna/fila. En el ejemplo puede verse que para la columna B, casillas B4 y B7, debe ir obligadamente un 9 en una de esas dos casillas, lo mismo ocurre para la columna D, casillas D1 y D4, y la columna H, casillas H1 y H7, por ese motivo en el resto de las casillas de las filas 1, 4 y 7 puede eliminarse el candidato 9, más precisamente de las casillas C7 y F4.
Medusa
Es como el Pez espada, pero con cuatro líneas (filas o columnas), es decir, cuatro filas (o columnas) que contienen cada una de ellas no más de cuatro casillas, con un candidato determinado, y compartiendo todas ellas no más de cuatro columnas (o filas). Estas forman una cuadrícula de hasta dieciséis casillas que son las únicas posibles para el candidato en esas cuatro filas (o columnas). Cualquier candidato que esté dentro de esas cuatro columnas (o filas), a excepción de las casillas de la cuadrícula, puede ser eliminado.
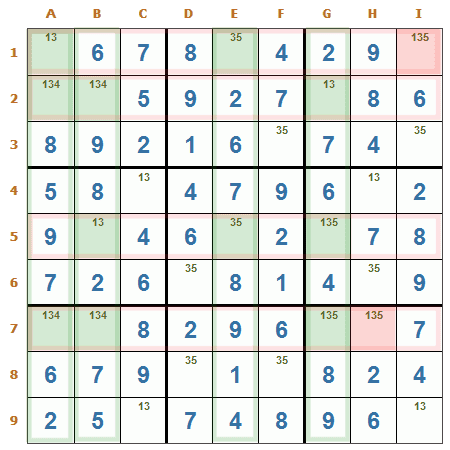
Medusa columna/fila. En el ejemplo puede verse que para la columna A, casillas A1, A2 y A7, debe ir obligadamente un 3 en una de esas tres casillas, lo mismo ocurre para la columna B, casillas B2, B5 y B7, para la columna E, casillas E1 y E5, y la columna G, casillas G2, G5 y G7, por ese motivo en el resto de las casillas de las filas 1, 2, 5 y 7 puede eliminarse el candidato 3, más precisamente de las casillas I1 y H7.
Cadenas coloreadas
Para aclarar este concepto primero veamos la siguiente definición:
Par conjugado: es cuando un número está como candidato en solo dos casillas dentro de un grupo (fila, columna o región). Ese número irá como valor en una de las dos casillas, pero no se sabe en cuál de las dos.
De forma indistinta, uno será llamado conjugado positivo y el otro conjugado negativo (paridad).
Cadenas coloreadas es cuando los pares conjugados (para un mismo candidato) se conectan entre sí. Hay que tener en cuenta que los conjugados de igual paridad (positiva o negativa) tienen el mismo estado (verdadero o falso).
Es muy útil usar dos colores, uno para marcar el conjugado positivo y otro para marcar el conjugado negativo.
Hay dos tipos de eliminación de candidatos para cadenas coloreadas:
Tipo 1
Si una casilla fuera de la cadena de paridad comparte un grupo (fila, columna o región) con un conjugado positivo y además, comparte otro grupo con un conjugado negativo, el candidato para esa casilla puede ser eliminado.
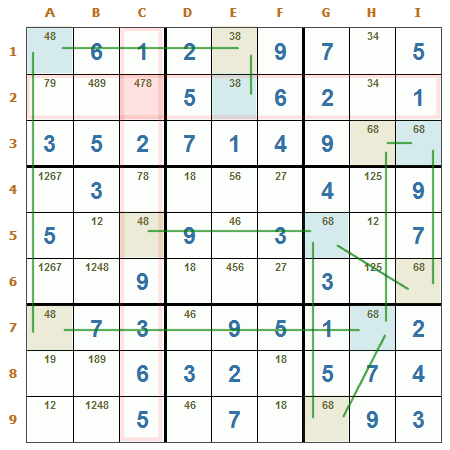
Cadena coloreada Tipo 1. En este ejemplo puede verse una cadena de pares conjugados para el candidato 8, las casillas de color celeste representan el conjugado positivo y las de color beige el conjugado negativo, las líneas verdes marcan la relación entre los pares conjugados. Hay que prestar atención a las casillas E2 y C5, estas tienen paridad opuesta. La casilla C2 comparte grupo con estas dos casillas (Fila 2 y Columna C), Por lo tanto, de esta casilla puede eliminarse con seguridad el candidato 8.
Tipo 2
Si un conjugado comparte un grupo con otro conjugado de la misma paridad, el candidato puede ser eliminado de todas las casillas conjugadas de esa paridad.
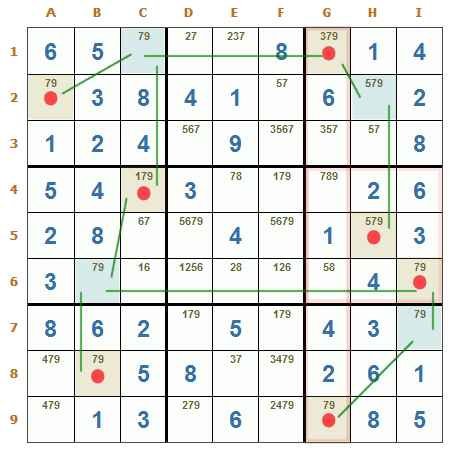
Cadena coloreada Tipo 2. Aquí la cadena de pares conjugados es para el candidato 9, las casillas de color celeste representan el conjugado positivo y las de color beige el conjugado negativo, las líneas verdes marcan la relación entre los pares conjugados. Hay que prestar atención a las casillas I6 y H5, estas comparten el grupo (región R6) y además, tienen igual paridad, por lo tanto, de todas las casillas de paridad negativa (marcadas con un círculo rojo) puede eliminarse con seguridad el candidato 9. También puede apreciarse que ocurre lo mismo con la columna G y las casillas G1 y G9.
Par remoto
Para aclarar este concepto primero veamos la siguiente definición:
En esencia, este método consiste en una cadena de pares desnudos conectados entre sí. Por grupo solo hay dos casillas con un par desnudo cada una, por lo tanto, entre ellas se establece una relación de casillas conjugadas, es decir en una casilla irá como valor uno de los candidatos y en la otra casilla irá el otro candidato, pero no se sabe cuál candidato irá en cual casilla. Una casilla será el conjugado positivo y la otra el conjugado negativo (paridad).
Si una casilla comparte un grupo con dos casillas conjugadas de diferente paridad, los candidatos del par desnudo pueden ser eliminados de esa casilla.
Veamos un ejemplo:
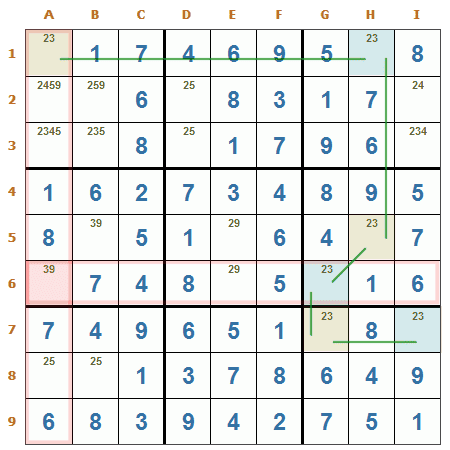
Par remoto. Aquí vemos una formación de pares desnudos (candidatos 2 y 3) encadenados, la paridad positiva está marcada con beige y la negativa con celeste, las líneas verdes marcan la relación entre las casillas. Si prestamos atención, la casilla A6 comparte grupo con las casillas G6 y A1 (Fila 6 y Columna A), y además, la paridad de esas casillas es opuesta, por lo tanto, en A6 se puede eliminar el 3 como candidato.
XY-wing
Dadas tres casillas con solo dos candidatos cada una:
la casilla 1 (c1) contiene un candidato llamado 'x' y el otro llamado 'y',
la casilla 2 (c2) contiene un candidato llamado 'x' y el otro llamado 'z',
la casilla 3 (c3) contiene un candidato llamado 'y' y el otro llamado 'z',
además, hay una relación de par conjugado entre las casillas c1 y c2 con el candidato 'x', y
también hay una relación de par conjugado entre las casillas c1 y c3 con el candidato 'y',
entonces en las casillas (a excepción de c1) que compartan simultáneamente un grupo con las casillas c2 y c3, se podrá eliminar el candidato 'z'.
Veamos un ejemplo:
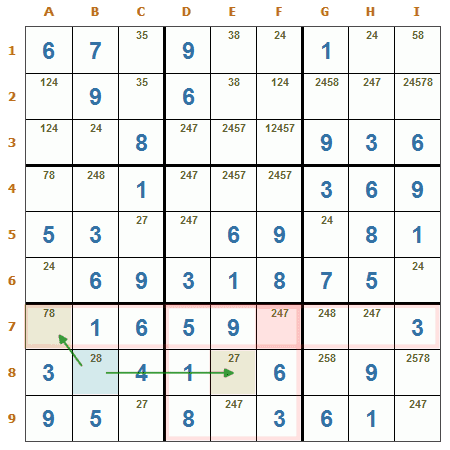
XY-wing. La casilla B8 tiene una relación de par conjugado con A7 para el candidato 8, y también tiene una relación de par conjugado con E8 para el candidato 2. Como la casilla F7 tiene un grupo en común con A7 y E8 (Fila 7 y Región R8), el candidato 7 (es el candidato común a estas dos casillas) puede ser eliminado de F7.
Esto se ve claramente analizándolo así:
Si B8 es un 8, A7 es un 7, entonces F7 NO puede ser 7.
Si B8 es un 2, E8 es un 7, entonces F7 NO puede ser 7.
En los dos casos F7 NO puede ser 7, con lo que puede ser eliminado como candidato.
XYZ-wing
Dadas tres casillas, una con tres candidatos y las otras con dos:
la casilla 1 (c1) contiene un candidato llamado 'x', otro llamado 'y' y el último llamado 'z',
la casilla 2 (c2) contiene un candidato llamado 'x' y el otro llamado 'z',
la casilla 3 (c3) contiene un candidato llamado 'y' y el otro llamado 'z',
además, hay una relación de par conjugado entre las casillas c1 y c2 con el candidato 'x', y
también hay una relación de par conjugado entre las casillas c1 y c3 con el candidato 'y',
entonces en las casillas que compartan simultáneamente un grupo con las casillas c1, c2 y c3, se podrá eliminar el candidato 'z'.
Veamos un ejemplo:
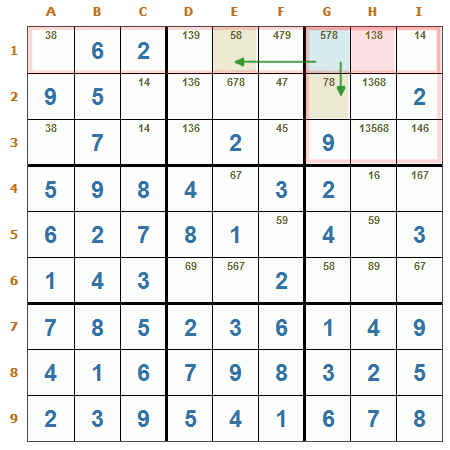
XYZ-wing. La casilla G1 tiene una relación de par conjugado con E1 para el candidato 5, y también tiene una relación de par conjugado con G2 para el candidato 7. Como la casilla H1 tiene un grupo en común con G1, E1 y G2 (Fila 1 y Región R3), el candidato 8 (es el candidato común a estas tres casillas) puede ser eliminado de H1.
Esto se ve claramente analizándolo así:
Si G1 es un 8, entonces H1 NO puede ser 8.
Si G1 es un 5, E1 es un 8, entonces H1 NO puede ser 8.
Si G1 es un 7, G2 es un 8, entonces H1 NO puede ser 8.
En los tres casos H1 NO puede ser 8, con lo que puede ser eliminado como candidato.
Cadena XY
Es una cadena compuesta de pares desnudos, donde cada grupo contiene un par conjugado con solo uno de los candidatos, además, la casilla inicial y final de la cadena (llamados extremos) tienen un candidato en común, llamado 'z'. Si una casilla fuera de la cadena comparte simultáneamente un grupo con las casillas extremos, el candidato 'z' puede ser eliminado de dicha casilla.
Veamos un ejemplo:
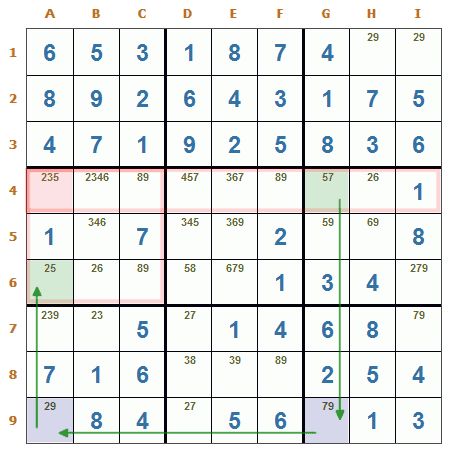
Cadena XY. La cadena comienza en G4, que tiene una relación de par conjugado con G9 para el candidato 7. Esta casilla a su vez tiene una relación de par conjugado con A9 para el candidato 9. Y esta tiene una relación de par conjugado con A6 con el candidato 2.
Los extremos de la cadena son las casillas G4 y A6 que tienen en común el candidato 5.
Como la casilla A4 tiene un grupo en común con los dos extremos (fila 4 y región 4), el candidato 5 se puede eliminar de esta casilla.
Esto se ve claramente analizándolo así:
Si G4 es 5, entonces A4 NO puede ser 5.
Si G4 es 7, G9 es 9, A9 es 2, A6 es 5, entonces A4 NO puede ser 5.
En los dos casos A4 NO puede ser 5, con lo que puede ser eliminado como candidato.
Rectángulo de unicidad
Primero recordemos que un sudoku válido tiene solución única. Definiremos ahora:
Patrón de unicidad: es cuando dos pares desnudos, formando un rectángulo, comparten exactamente dos filas, dos columnas y dos regiones. Se llama patrón de unicidad ya que esta figura tiene más de una solución, es decir forma un sudoku inválido.
El rectángulo de unicidad es un patrón de unicidad con candidatos extras en algunas de las cuatro casillas.
Tipo 1
Es un rectángulo de unicidad con candidatos extras en solo una de las cuatro casillas. Si estos candidatos extras se eliminaran quedaría formado un patrón de unicidad, es decir estos candidatos extras son obligatorios, por lo tanto, los dos candidatos del rectángulo, de esa casilla, pueden ser eliminados.

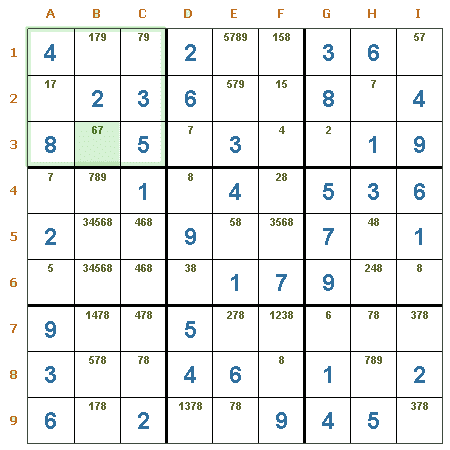
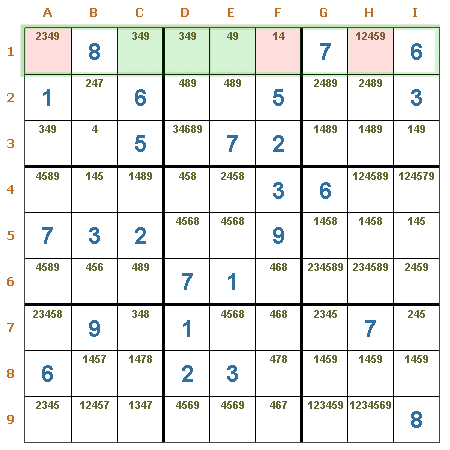
Rectángulo de unicidad Tipo 1. En este ejemplo puede verse la formación de un rectángulo de unicidad (figura en color rojo), que está formado por las casillas D2, D3, A2 y A3, si el candidato 2 se eliminara de A3 quedaría formado un patrón de unicidad, con lo cual quedaría un sudoku con más de una solución, de ello se desprende que el candidato 2 es obligatorio para esa casilla. Entonces se pueden eliminar los candidatos 6 y 9 de A3, quedando el 2 como valor.